Access answers to Maths MSBSHSE Solutions For SSC Part 1 Chapter 1 –Linear Equations in Two Variables

Practice set 1.1 Page no: 4

1. Complete the following activity to solve the simultaneous equations.

5x + 3y = 9 ……. (i)
2x + 3y = 12 ……… (ii)

Solution:

Given

5x + 3y = 9 ……. (i)

2x + 3y = 12 ……… (ii)

Subtracting equation (ii) from (i), we get,

(5x + 3y) –(2x + 3y) = 9 –125x –2x + 3y –3y

= -33x = -3x = -1

Putting the value of x in equation (i),

5(-1) + 3y = 9-5 + 3y = 93y = 14y = 14/3

Let’s add equations (I) and (II).

Hence, x = -1 and y = 14/3 is the solution of the equation.

2. Solve the following simultaneous equation.

(1) 3a + 5b = 26; a + 5b = 22

Solution:

3a + 5b = 26 …… (i)

a + 5b = 22 ………(ii)

Now by changing the sign of equation (ii) we get

–a – 5b = –22

Subtracting equation (ii) from (i) we get

2a = 4

a = 4/2

a = 2

Substituting a = 2 in equation (ii) we get

2 + 5b = 22

5b = 22 – 2

5b = 20

b = 20/5

b = 4

∴ solution is (a, b) = (2, 4)

(2) x + 7y = 10; 3x – 2y = 7

Solution:

Given

x + 7y = 10 ……. (i)

x – 2y = 7 ……… (ii)

Multiply equation (i) by 2 and equation (ii) by 7

2x + 14 y = 20

21x – 14 y = 49

Which implies

23 x = 69

x = 69/23

x = 3

Substituting x = 3 in equation (i)

3 + 7y = 10

7y = 10 – 3

7y = 7

y = 7/7

y = 1

∴ Solution is (x, y) = (3, 1)

(3)
2x – 3y = 9; 2x + y = 13

Solution:

Given

2x – 3y = 9 …… (i)

2x + y = 13 …… (ii)

To subtract equation (ii) from (i)

Change the sign of equation (ii)

2x – 3y = 9

-2x – y = –13

Which implies

–4y = –4

y = 4/4

y = 1

Substituting y = 1 in equation (ii)

2x + 1 = 13

2x = 13 –12x = 12x = 6

∴ solution is (x, y) = (1, 6)

(4) 5m – 3n = 19; m – 6n = –7

Solution:

Given

5m – 3n = 19 …… (i)

m – 6n = –7 …. (ii)

Multiply equation (ii) by 5

5m – 30n = -35 …. (iii)

Equating (i) and (iii), change the sign of equation (iii)

5m – 3n = 19

–5m + 30 n = 35

Adding both we get

27n = 54

n = 54/27

⇒ n = 2

Substituting n = 2 in equation (i)

⇒ 5m –3(2) = 19

⇒ 5m –6 = 19

⇒ 5m = 25

⇒ m = 5

∴ Solution is (m, n) = (5, 2)

(5) 5x + 2y = –3; x + 5y = 4

Solution:

5x + 2y = –3 …. (i)

x + 5y = 4 …… (ii)

Multiply equation (i) by 5 and equation (ii) by 2

25 x + 10 y = -15 …. (iii)

2x + 10 y = 8 …. (iv)

Change sign of equation (iv)

25 x + 10 y = -15

–2x –10 y = –8

23 x = -23

x = -1

Substituting x = –1 in equation (ii)

–1 + 5y = 4

5y = 4 + 1

5y = 5

Y = 1

∴ solution is (x, y) = (–1, 1)

(6)

Solution:

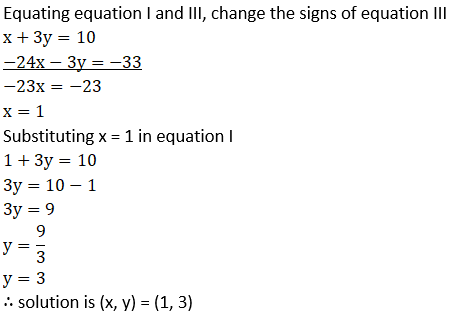
(7) 99x + 101 y = 499; 101x + 99y = 501

Solution:

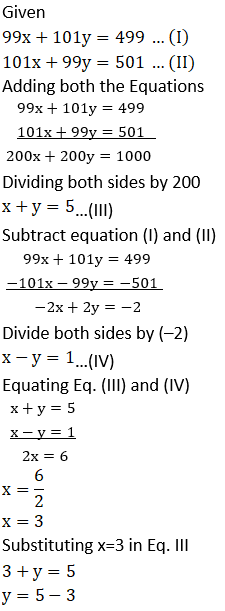
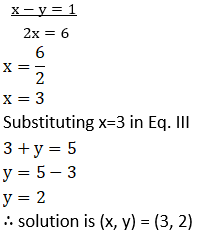
(8) 49x – 57y = 172; 57x – 49y = 252

Solution:

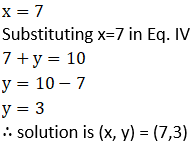
Practice set 1.2 Page no: 8

1. Complete the following table to draw graph of the equations

(I) x + y = 3

(II) x – y = 4

Solution:

(I) Given

x + y = 3 …. (i)

(i) Put value x=3 in equation (i)

We get, y = 3 –3

⇒ y = 0

ii. Put value y = 5 in equation (i)

We get, x = 3 – 5

⇒ x = -2

iii. Put value y = 3 in equation (i)

We get, x = 3 – 3

⇒ x = 0

Now the table becomes,

x	3	-2	0
y	0	5	3
(x, y)	(3, 0)	(-2, 5)	(0, 3)

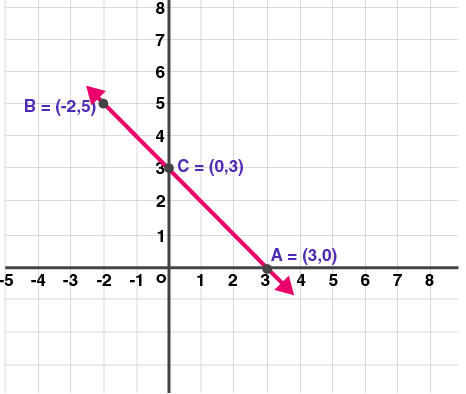
(2) Given

x – y = 4 ……. (ii)

i. Put value y = 0 in equation (ii)

we get, x = 4 – 0

⇒ x = 4

ii. Put value x = –1 in equation (ii)

we get, –y = 5

iii. Put value y = –4 in equation (ii)

we get, x = 4 + 4

⇒ x = 8

x	4	-1	0
y	0	-5	-4
(x, y)	(4, 0)	(-1, -5)	(0, -4)

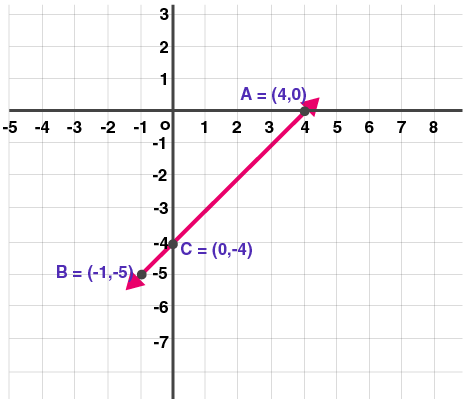
2. Solve the following simultaneous equations graphically.

(1) x + y = 6; x – y = 4

Solution:

Given x + y = 6 …. (i)

x	0	6	5
y	6	0	1
(x, y)	(0, 6)	(6, 0)	(5, 1)

x – y = 4 …… (ii)

x	0	2	5
y	-4	-2	1
(x, y)	(0, -4)	(2, -2)	(5, 1)

Calculating intersecting point

x + y = 6

x – y = 4

2x = 10

x = 10/2

x = 5

Putting x= 5 in equation (i)

5 + y = 6

y = 6 – 5

y = 1

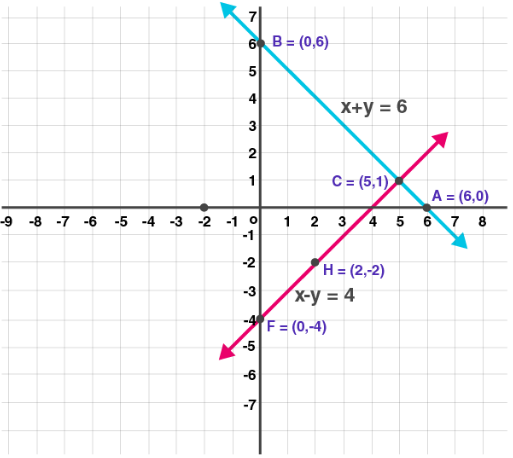
(2) x + y = 5; x – y = 3

Solution:

x + y = 5 …. (i)

x	0	2	4
y	5	3	1
(x, y)	(0, 5)	(2, 3)	(4, 1)

x – y = 3 ……(ii)

x	0	2	4
y	-3	-1	1
(x, y)	(0, -3)	(2, -1)	(4, 1)

Calculating intersecting point

x + y = 5

x – y = 3

which implies

2x = 8

x = 8/2

x = 4

Putting x= 4 in equation (i)

4 + y = 5

y = 5 – 4

y = 1

Intersection Point (4,1)

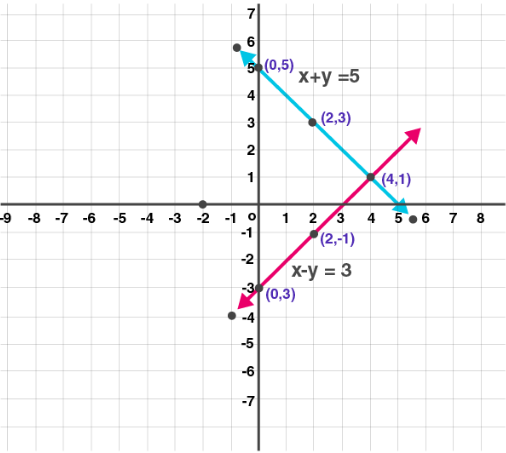
(3) x + y = 0; 2x – y = 9

Solution:

x + y = 0 …. (i)

x	1	3	5
y	-1	-3	-5
(x, y)	(1, -1)	(3, -3)	(5, -5)

2x – y = 9 …. (ii)

x	2	3	4
y	-5	-3	-1
(x, y)	(2, -5)	(3, -3)	(4, -1)

Calculating intersecting point

x + y = 0

2x – y = 9

3x = 9

x = 9/3

x = 3

Putting x= 3 in equation (i)

3 + y = 0

y = 0 – 3

y = -3

Intersection point (3, –3)

(4) 3x – y = 2; 2x – y = 3

Solution:

3x – y = 2 ……(i)

x	0	1	-1
Y	-2	1	-5
(x, y)	(0, -2)	(1, 1)	(-1, -5)

2x – y = 3 …… (ii)

x	3	2	-1
y	3	1	-5
(x, y)	(3, 3)	(2, 1)	(-1, -5)

Calculating intersecting point

3x – y = 2

–2x + y = -3

x = -1

Putting x= –1 in equation (i)

3× –1 – y = 2

–3 – y = 2

–y = 2 + 3

y = -5

Intersection point (–1, –5)

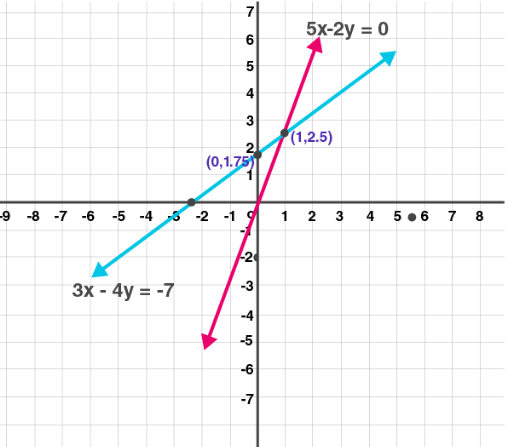
(5) 3x – 4y = –7; 5x – 2y = 0

Solution:

3x – 4y = 7 …. (i)

When x = 0, 4y = 7, y = 7/4

When y = 0, 3x = -7, x = -7/3

5x – 2y = 0 ……(ii)

When x = 0, y = 0

When x = 1, y = 5/2

Plotting both the graphs we get,

Calculating intersecting point

3x – 4y = -7

5x – 2y = 0

x = -1

Putting x= –1 in equation (i)

3 × –1 – y = 2

–3 – y = 2

–y = 2 + 3

y = –5

Intersection point (–1, –5)

 

practice set 1.3 Page no: 16

1. Fill in the blanks with correct number

Solution:

2. Find the values of following determinants.

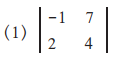
Solution:

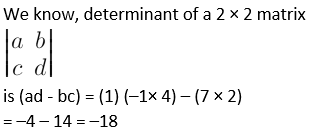
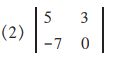
Solution:

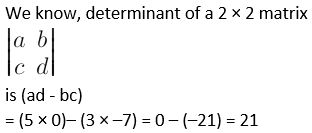
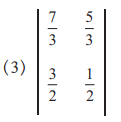
Solution:

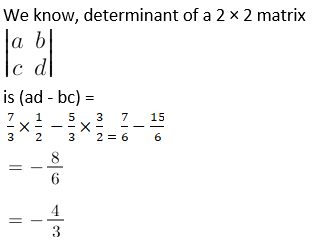
3. Solve the following simultaneous equations using Cramer’s rule.

(1) 3x – 4y = 10; 4x + 3y = 5

Solution:

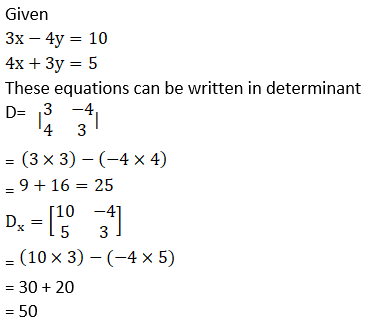
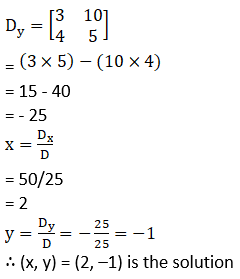
(2) 4x + 3y – 4 = 0; 6x = 8 – 5y

Solution:

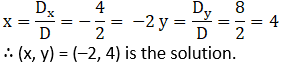
(3) x + 2y = –1; 2x – 3y = 12

Solution:

(4) 6x – 4y = –12; 8x – 3y = –2

Solution:

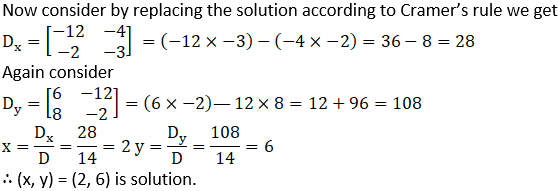
(5) 4m + 6n = 54; 3m + 2n = 28

Solution:

(6) 2x + 3y = 2; x – y/2 = ½

 

Solution:

Practice set 1.4 Page no: 19

1. Solve the following simultaneous equations.

Solution:

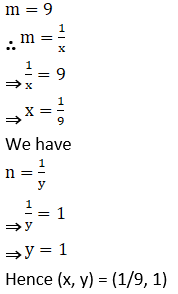
Solution:

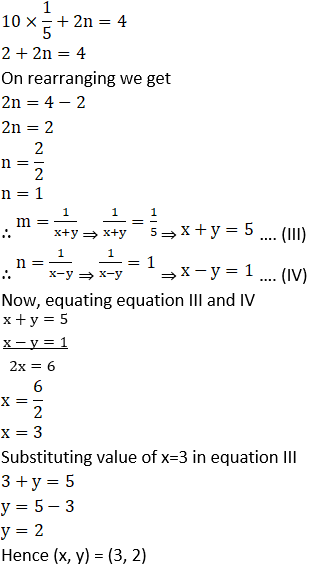
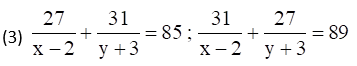
Solution:

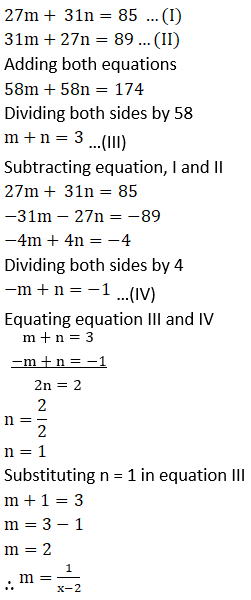
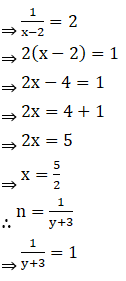
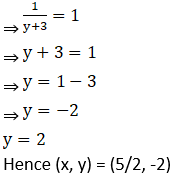
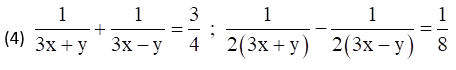
Solution:

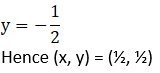
Practice set 1.5 Page no: 26

1. Two numbers differ by 3. The sum of twice the smaller number and thrice the greater number is 19. Find the numbers.

Solution:

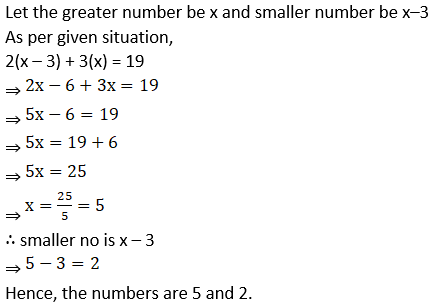
2. Complete the following.

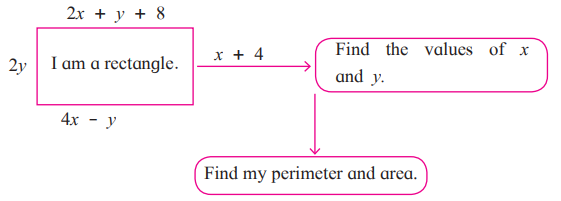
Solution:

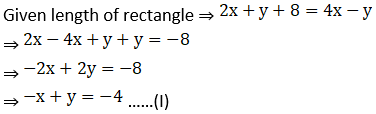
3. The sum of father’s age and twice the age of his son is 70. If we double the age of the father and add it to the age of his son the sum is 95. Find their present ages.

Solution:

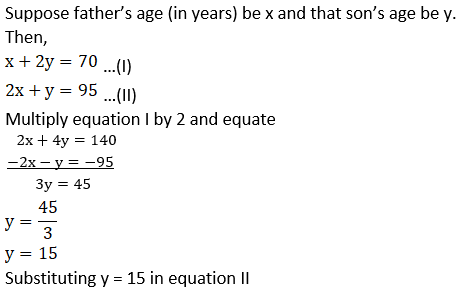
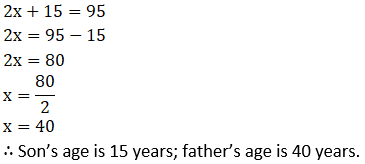
4. The denominator of a fraction is 4 more than twice its numerator. Denominator becomes 12 times the numerator, if both the numerator and the denominator are reduced by 6. Find the fraction.

Solution:

5. Two types of boxes A, B are to be placed in a truck having capacity of 10 tons. When 150 boxes of type A and 100 boxes of type B are loaded in the truck, it weighs 10 tons. But when 260 boxes of type A are loaded in the truck, it can still accommodate 40 boxes of type B, so that it is fully loaded. Find the weight of each type of box.

Solution:

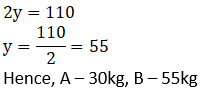
6. Out of 1900 km, Vishal travelled some distance by bus and some by aeroplane. Bus travels with average speed 60 km/hr and the average speed of aeroplane is 700 km/hr. It takes 5 hours to complete the journey. Find the distance, Vishal travelled by bus.

Solution:

Practice set 1.6 Page no: 27

1. Choose correct alternative for each of the following question
To draw graph of 4x+5y=19, Find y when x = 1.
A. 4
B. 3
C. 2
D. –3

Solution:

B. 3

Explanation:

2. For simultaneous equations in variables x and y, D_X = 49, D_Y = –63, D = 7, then what is x?
A. 7
B. –7
C. 1/7
D. -1/7

Solution:

A. 7

Explanation:

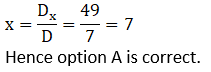
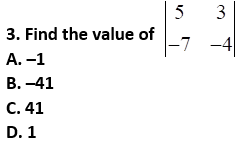
Solution:

D. 1

Explanation:

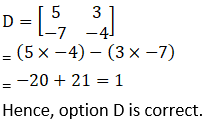
4. To solve x + y = 3; 3x–2y – 4 = 0 by determinant method find D.
A. 5
B. 1
C. –5
D. –1

Solution:

C. -5

Explanation:

5. ax + by = c and mx + ny = d and an ≠ bm then these simultaneous equations have –
A. Only one common solution.
B. No solution.
C. Infinite number of solutions.
D. Only two solutions.

Solution:

A. Only one common solution.

Explanation:

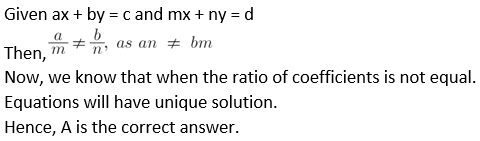
2. Complete the following table to draw the graph of 2x –6y = 3

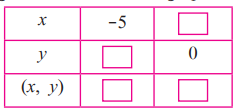
Solution:

Put x = –5, then

2 × -5 – 6y = 3

⇒ 3 + 10 = -6y

y = -13/6

Put y = 0, then

2x – 0 = 3

x = 3/2

x	-5	3/2
y	-13/6	0
(x, y)	(-5, -13/6)	(3/2, 0)

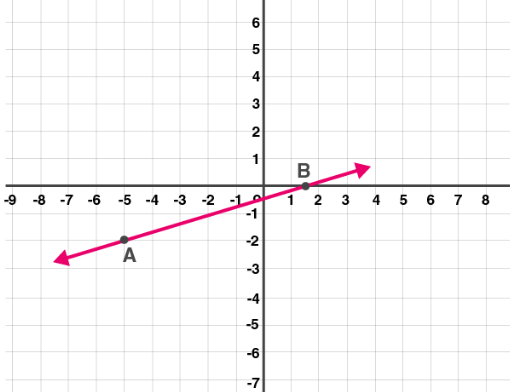
Where A = (-5, -13/6) and B = (3/2,0)

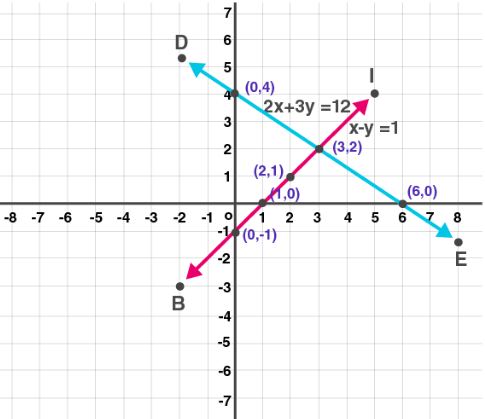
3. Solve the following simultaneous equation graphically.
(1) 2x + 3y = 12; x – y = 1

Solution:

Given

2x + 3y = 12

Substitute the values for x as shown in the table

x	0	6	3
y	4	0	2

Consider x – y = 1

x	1	0	2
y	0	-1	1

Now plot the graph as shown below:

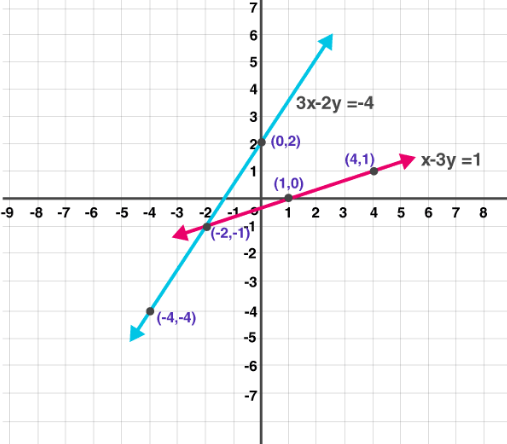
(2) x – 3y = 1; 3x – 2y + 4 = 0

Solution:

Given

x – 3y = 1

Substitute the values for x as shown in the table

x	-2	4	1
y	-1	1	0

Also given

3x – 2y + 4 = 0

x	0	-2	-4
y	2	-1	-1

Now plot the graph as shown below:

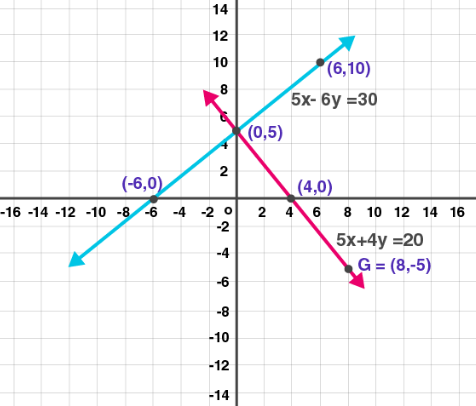
(3) 5x – 6y + 30 = 0; 5x + 4y – 20 = 0

Solution:

Given

5x – 6y + 30 = 0

Substitute the values for x as shown in the table

x	0	-6	6
y	5	0	10

Also given

5x + 4y –20 = 0

x	0	4	8
y	5	0	-5

Now plot the graph as shown below:

 

(4) 3x – y – 2 = 0; 2x + y = 8

Solution:

For equation 1, let ’s find the points for graph

3x –y –2 = 0

At x = 0

3(0) –y –2 = 0

⇒ y = -2

At x = 13

(1) –y –2 = 0

⇒ y = 1At x = 2

3(2) –y –2 = 0

⇒ 6 –y –2 = 0⇒ y =4

Hence, points for graph are (0, -1) (1, 1) and (2, 4)

For equation 22x + y = 8

At x = 0y = 8

at x = 12

(1) + y = 8

⇒ y = 6

at x =42(4) + y = 8

⇒ y = 0

Hence, points for graph are (0, 8) (1, 6) and (4, 0)

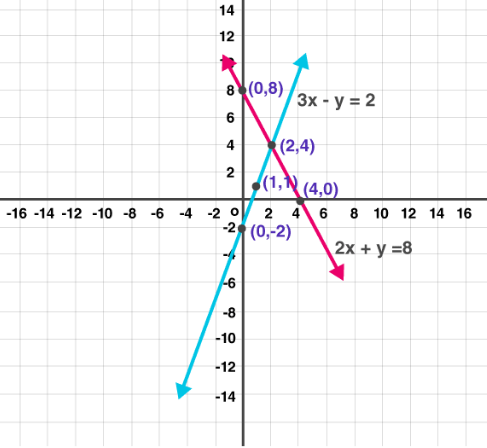
From graph, we observe both lines intersect at (2, 4)

Hence, x = 2 y = 4 is the solution of given pair

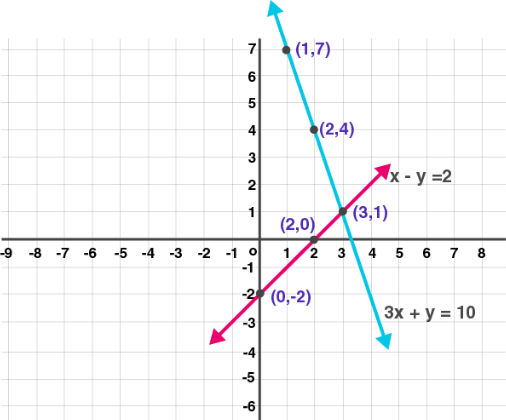
(5) 3x + y = 10; x – y = 2

Solution:

Given 3x + y = 10

x	1	2	3
y	7	4	1

Also, we have

x – y = 2

x	0	2	3
y	-2	0	1

Solving Both equations

4. Find the values of each of the following determinants.

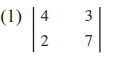
Solution:

Given

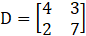
= (4 × 7) – (3 × 2) = 28 – 6 = 22

Solution:

Given

D =

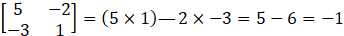
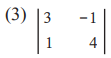
Solution:

Given

5. Solve the following equations by Cramer’s method.

(1) 6x – 3y = –10; 3x + 5y – 8 = 0

Solution:

(2) 4m – 2n = –4; 4m + 3n = 16

Solution:

Solution:

∴ (x, y) = (1/2, -1/2)

(4) 7x + 3y = 15; 12y – 5x = 39

Solution:

Solution:

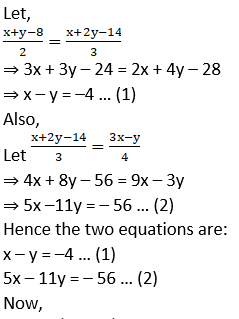
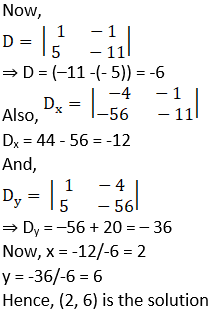
6. Solve the following simultaneous equations.

Solution:

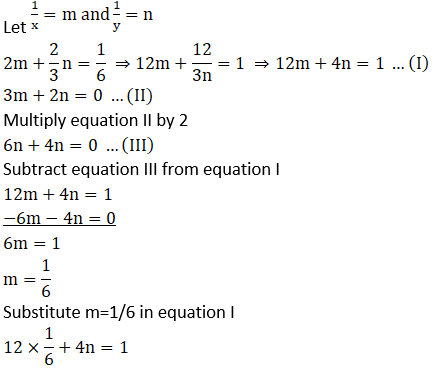
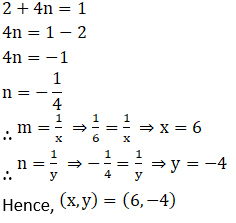
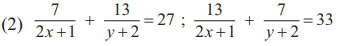
Solution:

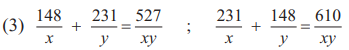
Solution:

Solution:

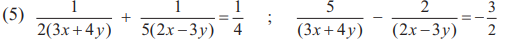
Solution:

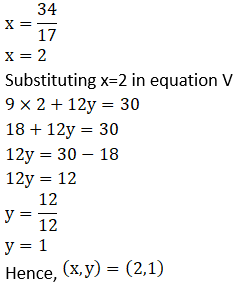
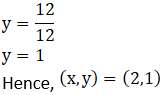
7. Solve the following word problems.

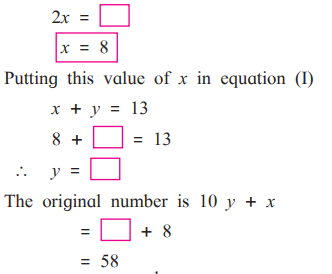
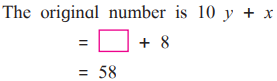
Solution:

2. Kantabai bought 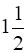kg tea and 5 kg sugar from a shop. She paid Rs 50 as return fare for rickshaw. Total expense was Rs 700. Then she realised that by ordering online the goods can be bought with free home delivery at the same price. So next month she placed the order online for 2 kg tea and 7 kg sugar. She paid Rs 880 for that. Find the rate of sugar and tea per kg.

Solution:

3. To find number of notes that Anushka had, complete the following activity

Solution:

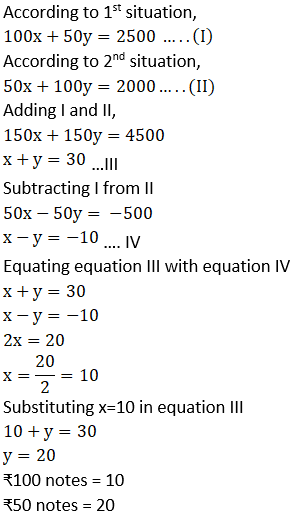
4. Sum of the present ages of Manish and Savita is 31. Manish’s age 3 years ago was 4 times the age of Savita. Find their present ages.

Solution:

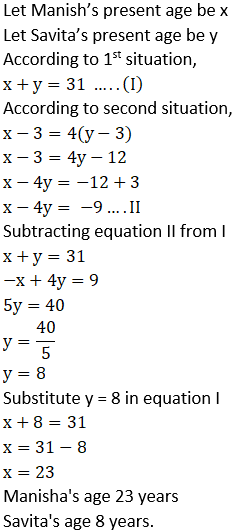
5. In a factory the ratio of salary of skilled and unskilled workers is 5: 3. Total salary of one day of both of them is ₹ 720. Find daily wages of skilled and unskilled workers.

Solution:

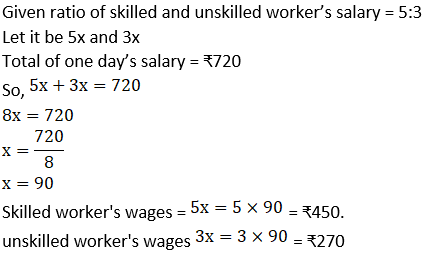
6. Places A and B are 30 km apart and they are on a straight road. Hamid travels from A to B on bike. At the same time Joseph starts from B on bike, travels towards A. They meet each other after 20 minutes. If Joseph would have started from B at the same time but in the opposite direction (instead of towards A) Hamid would have caught him after 3 hours. Find the speed of Hamid and Joseph.

Solution: